- homographique
-
homographique [ ɔmɔgrafik ] adj.• 1837; de homographie♦ Géom. Relatif à l'homographie. Figures homographiques. — Math. Fonction homographique : fonction définie par le quotient de deux fonctions du premier degré, et dont la courbe représentative est une hyperbole.
● homographique adjectif Qui concerne les homographes. ● homographique (expressions) adjectif Divisions homographiques, ensemble des points M et M′ homologues dans une homographie définie entre deux lignes L et L′, chacune portant la trajectoire d'un des points. Fonction homographique, fonction définie de C dans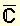 par :
par :
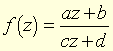 si z ≠ ∞ et
si z ≠ ∞ et 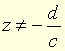 et
et 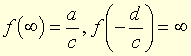 . (On précise fonction homographique propre lorsque ad − bc ≠ 0, f étant alors bijective, ou fonction homographique impropre lorsque ad − bc = 0, f étant alors une fonction constante.)
homographiqueadj. MATH Qui se rapporte à l'homographie. Fonction homographique, du type y = ax + b a'x + b'.⇒HOMOGRAPHIQUE, adj.GÉOM. [Correspond à homographie2] Qui est en relation d'homographie. Il [Fatou] a obtenu le résultat suivant : pour qu'un groupe de substitutions homographiques soit proprement discontinu, il faut et il suffit que la famille de ces fonctions homographiques soit normale et que toutes ses limites soient constantes (Gds cour. pensée math., 1948, p. 176). Il [Steiner] définit ainsi les coniques soit par l'intersection des rayons homologues de deux faisceaux homographiques, soit sous forme tangentielle. Chasles qui devança Steiner sur certains points contribua activement à la diffusion de ces méthodes concrètes et simples (Hist. gén. sc., t. 3, vol. 1, 1961, p. 25).Prononc. : [
. (On précise fonction homographique propre lorsque ad − bc ≠ 0, f étant alors bijective, ou fonction homographique impropre lorsque ad − bc = 0, f étant alors une fonction constante.)
homographiqueadj. MATH Qui se rapporte à l'homographie. Fonction homographique, du type y = ax + b a'x + b'.⇒HOMOGRAPHIQUE, adj.GÉOM. [Correspond à homographie2] Qui est en relation d'homographie. Il [Fatou] a obtenu le résultat suivant : pour qu'un groupe de substitutions homographiques soit proprement discontinu, il faut et il suffit que la famille de ces fonctions homographiques soit normale et que toutes ses limites soient constantes (Gds cour. pensée math., 1948, p. 176). Il [Steiner] définit ainsi les coniques soit par l'intersection des rayons homologues de deux faisceaux homographiques, soit sous forme tangentielle. Chasles qui devança Steiner sur certains points contribua activement à la diffusion de ces méthodes concrètes et simples (Hist. gén. sc., t. 3, vol. 1, 1961, p. 25).Prononc. : [ ]. Étymol. et Hist. 1837 géom. (CHASLES, Aperçu hist. orig. et développ. méth. géom., p. 261). Dér. de homographie; suff. -ique.homographique [ɔmɔgʀafik] adj.❖♦ Géom. Relatif à l'homographie. || Figures homographiques. — Fonction homographique : fonction, quotient de deux fonctions du premier degré, dont la courbe représentative est une hyperbole dont les asymptotes sont parallèles aux axes de coordonnées. || Relation homographique entre deux variables : relation du premier degré par rapport à chacune d'elles.
]. Étymol. et Hist. 1837 géom. (CHASLES, Aperçu hist. orig. et développ. méth. géom., p. 261). Dér. de homographie; suff. -ique.homographique [ɔmɔgʀafik] adj.❖♦ Géom. Relatif à l'homographie. || Figures homographiques. — Fonction homographique : fonction, quotient de deux fonctions du premier degré, dont la courbe représentative est une hyperbole dont les asymptotes sont parallèles aux axes de coordonnées. || Relation homographique entre deux variables : relation du premier degré par rapport à chacune d'elles.
Encyclopédie Universelle. 2012.
